Baby-Step, Giant-Step

Baby-Step, Giant-Step is an algorithm for computing the discrete logarithm in a given group.

The problem statement, that we are trying to solve, is the following. Given $g, a \in G$ for some finite group $G$ , where $g$ is a generator for $G$ , find the $x \in Z$ with $0 \leq x < | G |$ such that:

g^{x} = a .

Which is to say, we are evaluating $\log_{g} (a)$ .

Motivation, and Description of Method

Naively, one might consider calculating powers of the primitive root $g$ until the output $a$ has been found. Baby-Step, Giant-Step begins with this, however we only calculate roots up to and not including $⌈ \sqrt{n} ⌉$ . These calculations are the baby steps from the name of the algorithm.

If we happen to find $a$ already, then we are done, however this is unlikely.

Consider all consecutive powers of the primitive root listed in order as in the diagram below:

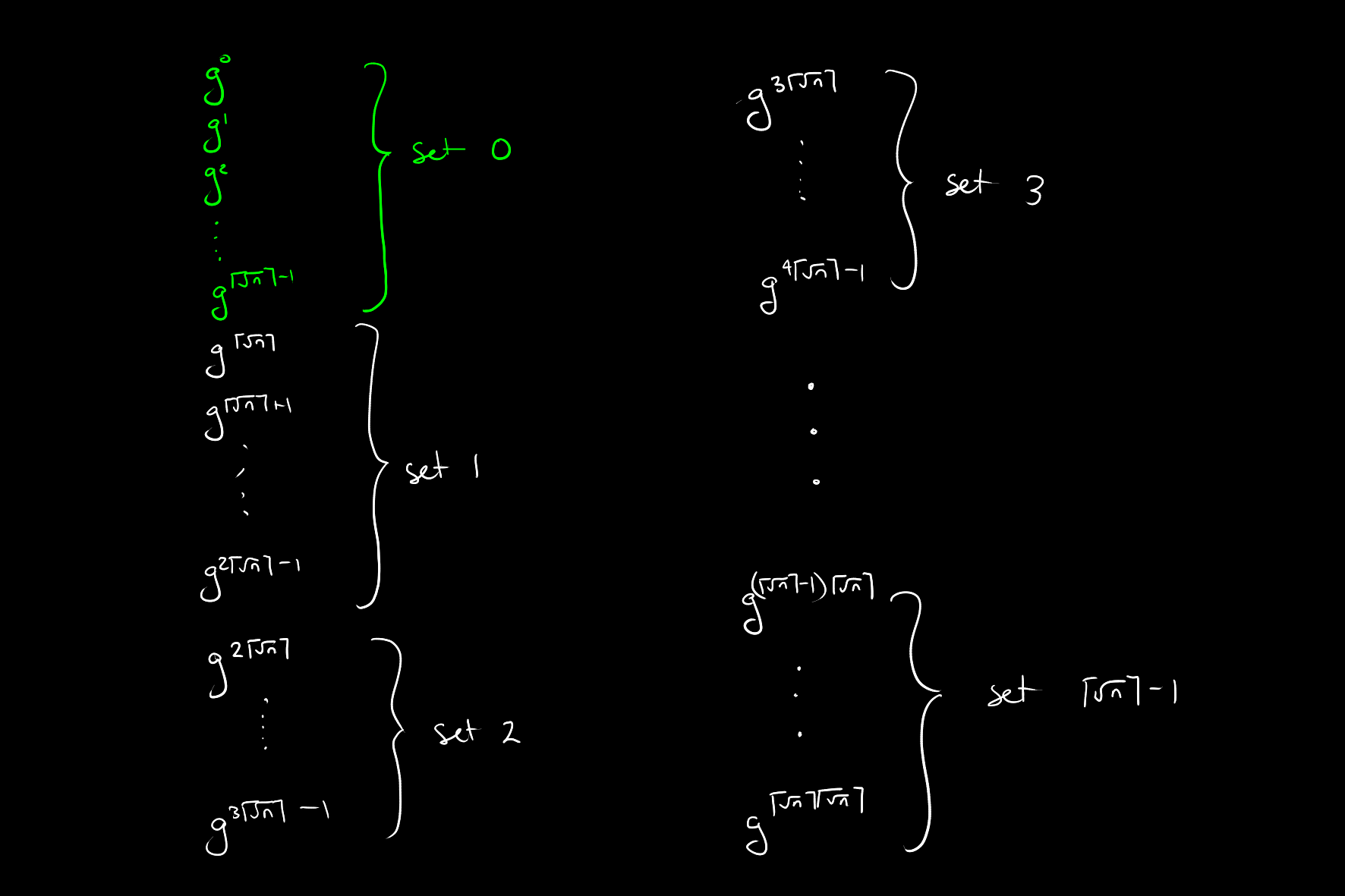
These are organised into sets of size $⌈ \sqrt{n} ⌉$ and there are $⌈ \sqrt{n} ⌉$ such sets, which means we have $⌈ \sqrt{n} ⌉ ⌈ \sqrt{n} ⌉ \geq n$ total powers, so there may be some overlap at the end.

Set $0$ corresponds with the initial powers we calculated in the baby steps. Then, we compute $g^{- ⌈ \sqrt{n} ⌉}$ .

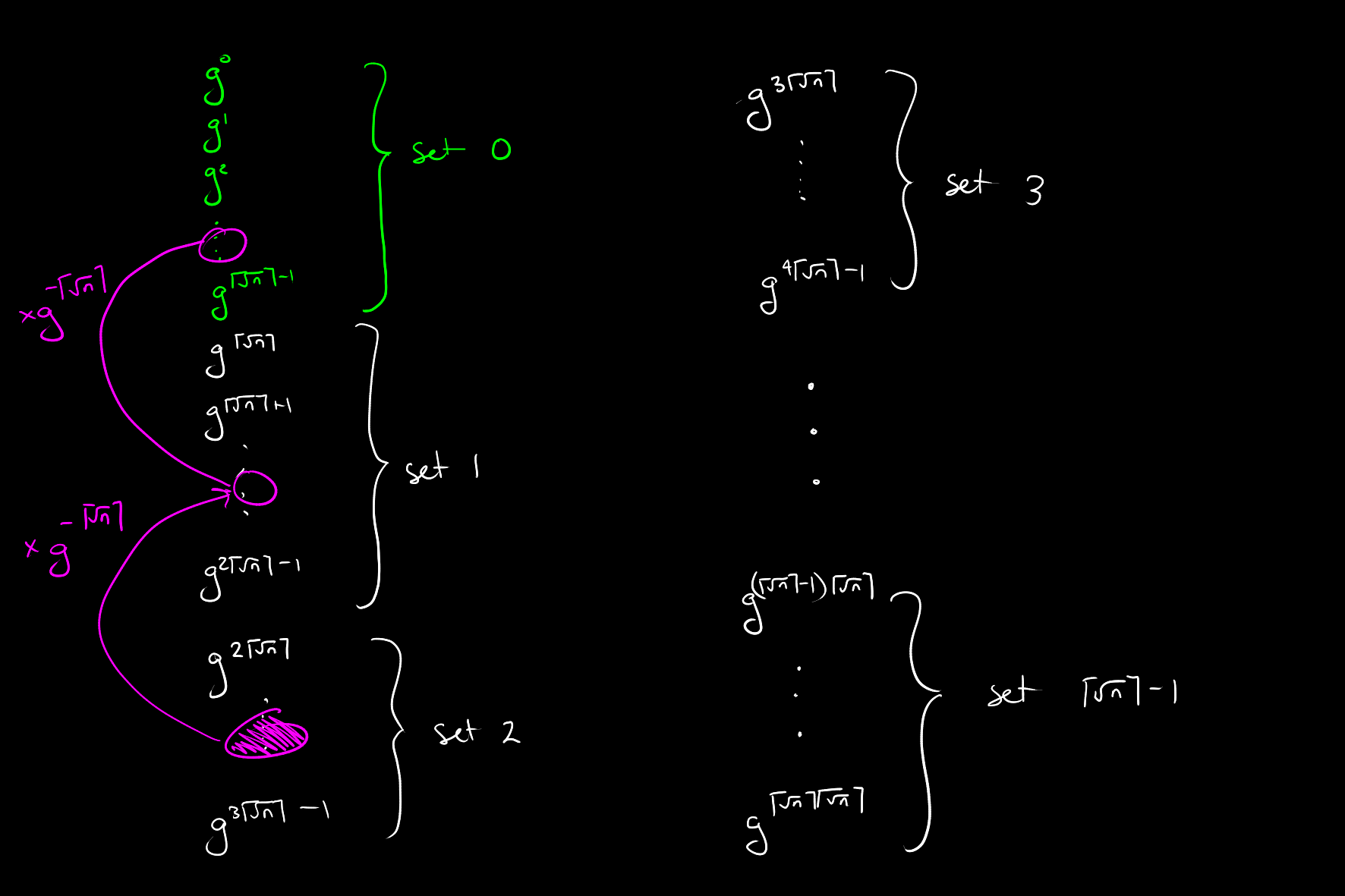
We now take the giant steps. Consider that $a$ is at the shaded pink circle below in set $3$ . In that case, $g^{- ⌈ \sqrt{n} ⌉} a$ puts it in set $2$ . In general, this shifts an element from set $k$ to set $k - 1$ (except of course at set $0$ ). After this multiplication, we check if it's in the pre-calculated set $0$ , if not, we repeat until it is.

Once it is, we know at that point that $a$ multiplied by some power of $g^{- ⌈ \sqrt{n} ⌉}$ (where the power is given by the number of giant steps we took) is another known power of $g$ . This then makes it easy to solve for $a$ . Specifically, if $i$ is the number of giant steps, and $j$ is the corresponding power in set $0$ :

a (g^{- ⌈ \sqrt{n} ⌉})^{i} = g^{j} ⟹ a = g^{j + i ⌈ \sqrt{n} ⌉} .

Example

Solve

5^{x} = 12 (\mod 17) .

First note that in this case our group is of order $16$ . As such we need to compute the first $⌈ \sqrt{15} ⌉$ following powers as follows:

\begin{aligned} 5^{0} & \equiv 1 (\mod 17) \\ 5^{1} & \equiv 5 (\mod 17) \\ 5^{2} & \equiv 8 (\mod 17) \\ 5^{3} & \equiv 6 (\mod 17) \end{aligned}

Since we did not find $17$ , we now need to take our desired result of $12$ and multiply by $5^{- 4}$ . The best way to compute this depends on our group, in this case we can solve

5^{4} \cdot h = 1 (\mod 17)

using the extended euclidean algorithm, where $5^{4} = 5 \cdot 5^{3}$ , the latter of which we have already computed.

This results in $h = 5^{- 4} = 4$ .

We then have

\begin{aligned} 12 \cdot 4 & \equiv 14 (\mod 17) \\ 14 \cdot 4 & \equiv 5 (\mod 17) \end{aligned}

Since we know that $5 = 5^{1}$ (i.e. it appears on our first list of powers), we have that

12 \cdot 4^{2} \equiv 5^{1} ⟹ 12 \cdot (5^{- 4})^{2} \equiv 5 ⟹ 12 \equiv 5^{9} .

Implementation

Here is an implementation of the algorithm in the specific case where the underlying group is the group of units modulo $n$ .

fn main() {
    println!("{}", baby_step_giant_step(13, 2, 3));
}

fn modular_exponent(base : u64, power : u64, modulus : u64) -> u64 {
    let mut result = 1;
    for _ in 0..power {
        result *= base % modulus;
    }

    result % modulus
}

/// We must have that:
/// - `modulus` is `prime`
/// - primitive_root is actually a primitive_root modulo `modulus`
/// - `logarithm` is some positive integer
/// This then computers `power` such that:
/// `primitive_root`^`power` = `logarithm` (mod `modulus`)
fn baby_step_giant_step(modulus : u64, primitive_root : u64, logarithm : u64) -> u64 {
    // Since modulus is prime, phi(modulus) = modulus - 1
    let group_order = modulus - 1;

    let m = (group_order as f64).sqrt() as u64 + 1;

    // Compute initial powers of the primitive_root (up to floor(sqrt(group_order)))
    let powers = {
        let mut powers = std::collections::HashMap::with_capacity(m as usize);

        let mut power = 1;
        for j in 0..m {
            powers.insert(power, j);
            power *= primitive_root % modulus;
        }

        powers
    };

    let mut guess = logarithm % modulus;
    for i in 0..m {
        match powers.get(&guess) {
            Some(power) => {
                return i * m + power;
            },
            None => {
                guess = (guess * modular_exponent(primitive_root, group_order - m, modulus)) % modulus;
            },
        }
    }

    unreachable!()
}